 Illustration of BOMCT
Illustration of BOMCTAbstract
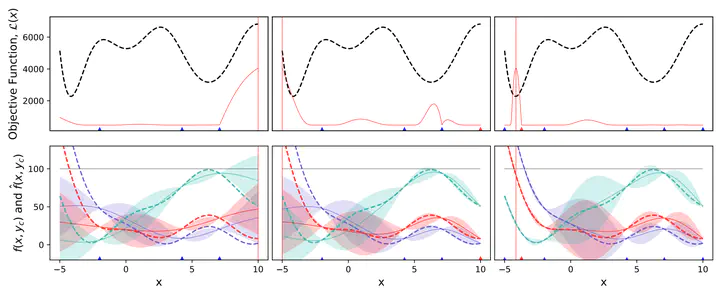
Bayesian optimization (BO) that employs the Gaussian process (GP) as a surrogate model has recently gained much attention in optimization of expensive black-box functions. In BO, the number of experiments necessary to optimize a function can be considerably reduced by sequentially selecting next design points that are optimal with respect to some sampling criterion. However, little research has been done to address the optimization of a multiple-component system where each component has a certain target value to meet. In this paper, we aim to find an optimal design parameter in the sense that the response function is close to the target value for every component. To this end, the squared errors from the targets are aggregated to produce an objective function. Instead of modeling this objective using GP as in the standard BO formulation, we place the GP prior over the response function. As a result, the distribution over the objective function follows that of the weighted sum of non-central chi-squared random variables (WSNC) due to the inter-dependency between responses. When components of the system are changed, the standard BO suffers inefficiency; however, our formulation enables us to retain a learned model, resulting in better efficiency. We compare the rates of convergence of different BO methods and other black-box optimization baselines using several test functions. The performance of our model is comparable to the standard BO when there is no change in the system, but the superiority of our method becomes clear when changes in the components occur.