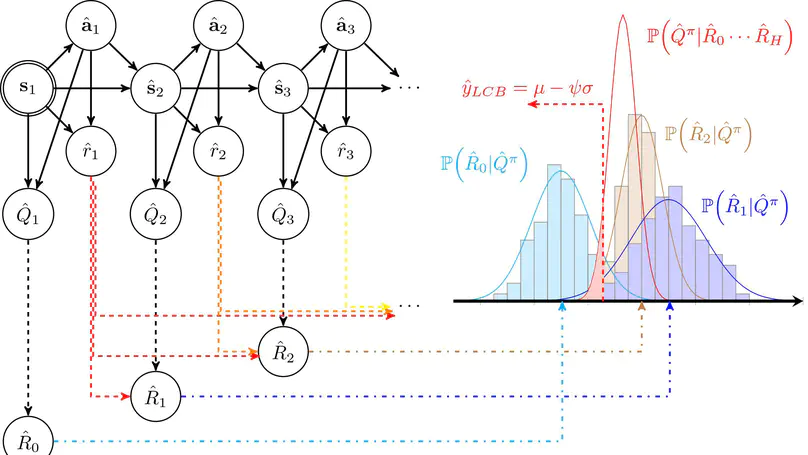
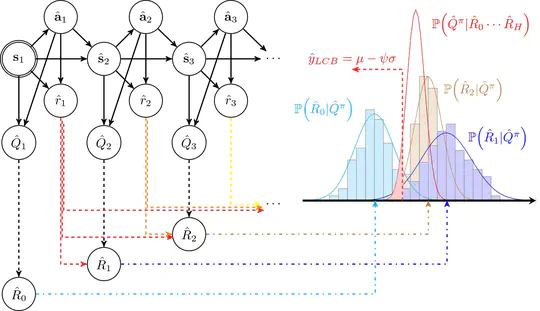
A model-based offline RL algorithm that is able to trade-off the uncertainty of the learned dynamics model with that of the value function through Bayesian posterior estimation, achieving state-of-the-art performance on a variety of D4RL benchmark tasks.

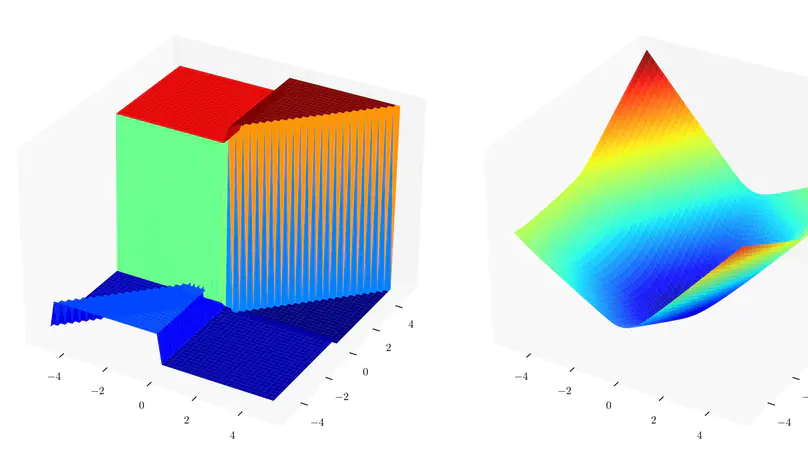
The Smart Predict+Optimize (SPO) framework tries to solve a decision-making problem expressed as mathematical optimization in which some coefficients have to be estimated by a predictive model. The challenge is that this problem is non-convex and non-differentiable, even for linear programs with linear predictive models. Despite that, we provide the first exact optimal solution to the SPO problem by formulating it as a bi-level bi-linear program and reducing it to a mixed-integer linear program (MILP) using a novel symbolic method.

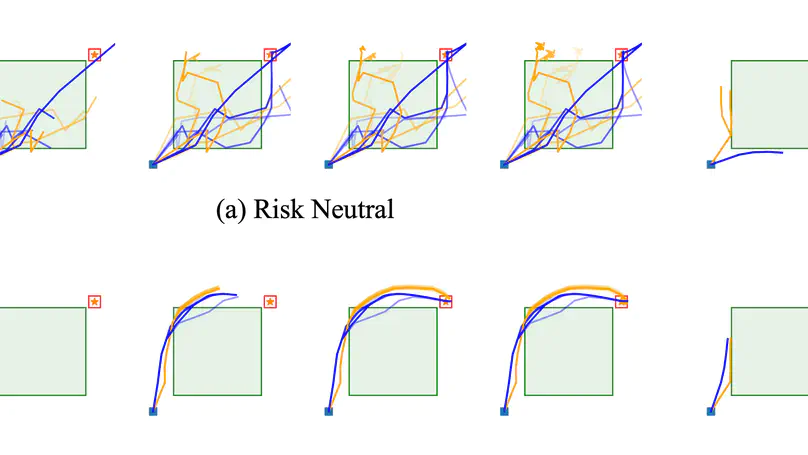
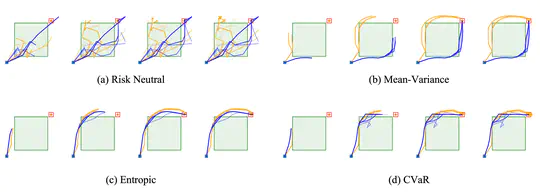
End-to-end planning framework for risk-sensitive planning under stochastic environments by backpropagating through a model of the environment. The core idea is to use reparameterization of the state distribution, leading to a unique distributional perspective of end-to-end planning where the return distribution is utilized for sampling as well as optimizing risk-aware objectives by backpropagation in a unified framework.

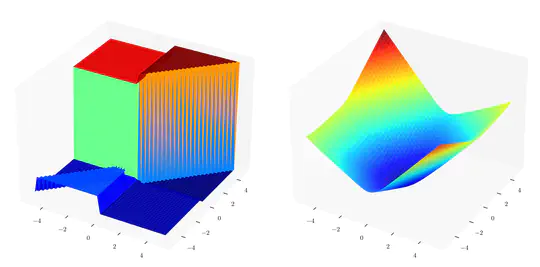
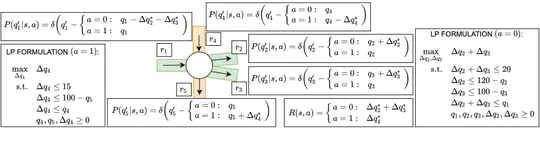
Recent advances in symbolic dynamic programming (SDP) have significantly broadened the class of MDPs for which exact closed-form value functions can be derived. However, no existing solution methods can solve complex discrete and continuous state MDPs where a linear program determines state transitions — transitions that are often required in problems with underlying constrained flow dynamics arising in problems ranging from traffic signal control to telecommunications bandwidth planning. In this paper, we present a novel SDP solution method for MDPs with LP transitions and continuous piecewise linear dynamics by introducing a novel, fully symbolic argmax operator.