Symbolic Dynamic Programming for Continuous State MDPs with Linear Program Transitions

Abstract

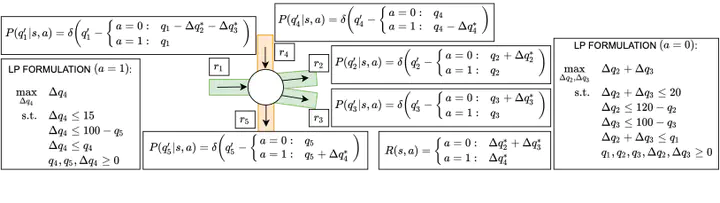
Recent advances in symbolic dynamic programming (SDP) have significantly broadened the class of MDPs for which exact closed-form value functions can be derived. However, no existing solution methods can solve complex discrete and continuous state MDPs where a linear program determines state transitions — transitions that are often required in problems with underlying constrained flow dynamics arising in problems ranging from traffic signal control to telecommunications bandwidth planning. In this paper, we present a novel SDP solution method for MDPs with LP transitions and continuous piecewise linear dynamics by introducing a novel, fully symbolic argmax operator. On three diverse domains, we show the first automated exact closed-form SDP solution to these challenging problems and the significant advantages of our SDP approach over discretized approximations.